Iris subspecies classification¶
Notebook Cell
import pandas as pd
import seaborn as sns
from sklearn import tree
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix, classification_report, roc_auc_score
import matplotlib.pyplot as plt
iris_df = sns.load_dataset('iris')---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 import pandas as pd
2 import seaborn as sns
3 from sklearn import tree
ModuleNotFoundError: No module named 'pandas'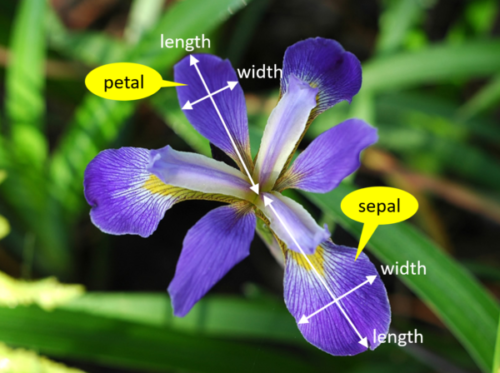
We’re trying to build an automatic flower classifier that, for measurements of a new flower returns the predicted species. To do this, we have a dataset with columns for species, petal width, petal length, sepal length, and sepal width. The species is what type of flower it is the petal and sepal are parts of the flower.
To start we will look at the data
Source
iris_df.head()Notebook Cell
iris_df.columnsThe species will be the target and the measurements will be the features. We want to predict the target from the features, the species from the measurements.
feature_vars = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
target_var = 'species'What does Naive Bayes do?¶
- Naive = indepdent features
- Bayes = most probable
More resources:
We can look at this data using a pair plot. It plots each pair of numerical variables in a grid of scatterplots and on the diagonal (where it would be a variable with itself) shows the distribution of that variable.
sns.pairplot(data =iris_df,hue=target_var)This data is reasonably separable beacuse the different species (indicated with colors in the plot) do not overlap much. We see that the features are distributed sort of like a normal, or Gaussian, distribution. In 2D a Gaussian distribution is like a hill, so we expect to see more points near the center and fewer on the edge of circle-ish blobs. These blobs are slightly live ovals, but not too skew.
This means that the assumptions of the Gaussian Naive Bayes model are met well enough we can expect the classifier to do well.
Separating Training and Test Data¶
To do machine learning, we split the data both sample wise (rows if tidy) and variable-wise (columns if tidy). First, we’ll designate the columns to use as features and as the target.
The features are the input that we wish to use to predict the target.
Next, we’ll use a sklearn function to split the data randomly into test and train portions.
X_train, X_test, y_train, y_test = train_test_split(iris_df[feature_vars],
iris_df[target_var],
random_state=5)This function returns multiple values, the docs say that it returns twice as many as it is passed. We passed two separate things, the features and the labels separated, so we get train and test each for both.
X_train.head()X_train.shape, X_test.shapeWe can see by default how many samples it puts the training set:
len(X_train)/len(iris_df)So by default we get a 75-25 split.
Instantiating our Model Object¶
Next we will instantiate the object for our model. In sklearn they call these objects estimator. All estimators have a similar usage. First we instantiate the object and set any hyperparameters.
Instantiating the object says we are assuming a particular type of model. In this case Gaussian Naive Bayes. This sets several assumptions in one form:
- we assume data are Gaussian (normally) distributed
- the features are uncorrelated/independent (Naive)
- the best way to predict is to find the highest probability (Bayes)
this is one example of a Bayes Estimator
Gaussian Naive Bayes is a very simple model, but it is a generative model (in constrast to a discriminative model) so we can use it to generate synthetic data that looks like the real data, based on what the model learned.
gnb = GaussianNB()At this point the object is not very interesting
gnb.__dict__The fit method uses the data to learn the model’s parameters. In this case, a Gaussian distribution is characterized by a mean and variance; so the GNB classifier is characterized by one mean and one variance for each class (in 4d, like our data)
gnb.fit(X_train,y_train)The attributes of the estimator object (gbn) describe the data (eg the class list) and the model’s parameters. The theta_ (often in math as θ or μ)
represents the mean and the var_ (σ) represents the variance of the
distributions.
gnb.__dict__Scoring a model¶
Estimator objects also have a score method. If the estimator is a classifier, that score is accuracy. We will see that for other types of estimators it is different types.
gnb.score(X_test,y_test)Making model predictions¶
we can predict for each sample as well:
y_pred = gnb.predict(X_test)We can also do one single sample, the iloc attrbiute lets us pick out rows by
integer index even if that is not the actual index of the DataFrame
X_test.iloc[0]but if we pick one row, it returns a series, which is incompatible with the predict method.
gnb.predict(X_test.iloc[0])If we select with a range, that only includes 1, it still returns a DataFrame
X_test.iloc[0:1]which we can get a prediction for:
gnb.predict(X_test.iloc[0:1])We can also pass a 2D array (list of lists) with values in it that were never in our dataset at all (here I typed in values similar to the mean for setosa above)
gnb.predict([[5.1, 3.6, 1.5, 0.25]])This way it warns us that the feature names are missing, but it still gives a prediction.
Evaluating Performance in more detail¶
confusion_matrix(y_test,y_pred)This is a little harder to read than the 2D version but we can make it a dataframe to read it better.
n_classes = len(gnb.classes_)
prediction_labels = [['predicted class']*n_classes, gnb.classes_]
actual_labels = [['true class']*n_classes, gnb.classes_]
conf_mat = confusion_matrix(y_test,y_pred)
conf_df = pd.DataFrame(data = conf_mat, index=actual_labels, columns=prediction_labels)Notebook Cell
c1 = gnb.classes_[1]
c2 = gnb.classes_[2]
conf12 = conf_mat[1][2]Unexecuted inline expression for: conf12 flowers were mistakenly classified as Unexecuted inline expression for: c1 when they were really Unexecuted inline expression for: c2
This report is also available:
print(classification_report(y_test,y_pred))We can also get a report with a few metrics.
- Recall is the percent of each species that were predicted correctly.
- Precision is the percent of the ones predicted to be in a species that are truly that species.
- the F1 score is combination of the two
We see we have perfect recall and precision for setosa, as above, but we have lower for the other two because there were mistakes where versicolor and virginica were mixed up.
N = 20
n_features = len(feature_vars)
gnb_df = pd.DataFrame(np.concatenate([np.random.multivariate_normal(th, sig*np.eye(n_features),N)
for th, sig in zip(gnb.theta_,gnb.var_)]),
columns = gnb.feature_names_in_)
gnb_df['species'] = [ci for cl in [[c]*N for c in gnb.classes_] for ci in cl]
sns.pairplot(data =gnb_df, hue='species')To break this code down:
To do this, we extract the mean and variance parameters from the model
(gnb.theta_,gnb.sigma_) and zip them together to create an iterable object
that in each iteration returns one value from each list (for th, sig in zip(gnb.theta_,gnb.sigma_)).
We do this inside of a list comprehension and for each th,sig where th is
from gnb.theta_ and sig is from gnb.sigma_ we use np.random.multivariate_normal
to get 20 samples. In a general multivariate normal distribution the second parameter is actually a covariance
matrix. This describes both the variance of each individual feature and the
correlation of the features. Since Naive Bayes is Naive it assumes the features
are independent or have 0 correlation. So, to create the matrix from the vector
of variances we multiply by np.eye(4) which is the identity matrix or a matrix
with 1 on the diagonal and 0 elsewhere. Finally we stack the groups for each
species together with np.concatenate (like pd.concat but works on numpy objects
and np.random.multivariate_normal returns numpy arrays not data frames) and put all of that in a
DataFrame using the feature names as the columns.
Then we add a species column, by repeating each species 20 times
[c]*N for c in gnb.classes_ and then unpack that into a single list instead of
as list of lists.
How does it make the predictions?¶
It computes the probability for each class and then predicts the highest one:
gnb.predict_proba(X_test)we can also plot these
# make the probabilities into a dataframe labeled with classes & make the index a separate column
prob_df = pd.DataFrame(data = gnb.predict_proba(X_test), columns = gnb.classes_ ).reset_index()
# add the predictions
prob_df['predicted_species'] = y_pred
prob_df['true_species'] = y_test.values
# for plotting, make a column that combines the index & prediction
pred_text = lambda r: str( r['index']) + ',' + r['predicted_species']
prob_df['i,pred'] = prob_df.apply(pred_text,axis=1)
# same for ground truth
true_text = lambda r: str( r['index']) + ',' + r['true_species']
prob_df['correct'] = prob_df['predicted_species'] == prob_df['true_species']
# a dd a column for which are correct
prob_df['i,true'] = prob_df.apply(true_text,axis=1)
prob_df_melted = prob_df.melt(id_vars =[ 'index', 'predicted_species','true_species','i,pred','i,true','correct'],value_vars = gnb.classes_,
var_name = target_var, value_name = 'probability')
prob_df_melted.head()and then we can plot this:
# plot a bar graph for each point labeled with the prediction
sns.catplot(data =prob_df_melted, x = 'species', y='probability' ,col ='i,true',
col_wrap=5,kind='bar', hue='species')GPT3¶
For GPT3 they trained a model to represent the base training data well and then fine-tuned it on question-answer datasets. Conceptually, they trained it to fill in the next missing word, by taking blocks of the training data, removing a word, and training the model to predict the correct word (the one they had removed).
This means, that conceptually, the goal of LLMs is to predict the next token given a sequence of tokens.